2 數(shù)值計(jì)算程序及網(wǎng)格的有效驗(yàn)證

本文對液橋的三維網(wǎng)格進(jìn)行了有效性驗(yàn)證，最終采用60×68×60的非均勻計(jì)算網(wǎng)格。為了驗(yàn)證計(jì)算程序的可靠性，本文對Vizman et al。文中的Rayleigh-Bénard結(jié)構(gòu)的算例進(jìn)行了重復(fù)。(采用導(dǎo)電的鎵熔體材料的相關(guān)參數(shù)為:密度ρ=6。1×10^3 kg/m^3，熱膨脹系數(shù)β=1。26×10^-4 /K，動力學(xué)粘度ν=1。907×10^-7 kg/ms，擴(kuò)散系數(shù)κ_T=9。22×10^-6 kg/ms，電導(dǎo)率σ=3。87×10^6 A/Vm)。圖2為二極對非均勻旋轉(zhuǎn)磁場下，本文計(jì)算得到的熔體在r=3R/4處周向方向的洛倫茲力的分布曲線(a)和文獻(xiàn)結(jié)果(b)。由圖可知，熔體在r=3R/4處熔體周向的洛倫茲力呈拋物線型分布，并在z=0。5H處達(dá)到最大值。本文的計(jì)算結(jié)果與Vizman et al。的結(jié)果較好地吻合，且計(jì)算所得的周向洛倫茲力的最大值與Vizman et al。通過數(shù)值計(jì)算和實(shí)驗(yàn)得到的最大值的相對誤差為1。8%。該結(jié)果驗(yàn)證了本文計(jì)算程序的可靠性。

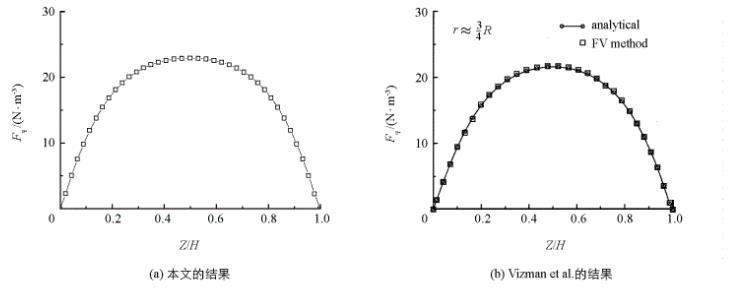
(a) 本文的結(jié)果 (b) Vizman et al的結(jié)果

圖2 熔體在半徑為r=3R/4處沿其軸向方向的周向洛倫茲力分布

3 結(jié)果及分析

為了深入分析外加非均勻旋轉(zhuǎn)磁場對液橋熔體對流的控制作用，本文數(shù)值研究了微重力環(huán)境下，二極對非均勻旋轉(zhuǎn)磁場對三維半浮區(qū)液橋表面張力對流的影響。文中相關(guān)參數(shù)的取值:旋轉(zhuǎn)磁場強(qiáng)度7 mT，旋轉(zhuǎn)頻率50 Hz;相應(yīng)的無量綱量參數(shù)Pr=0。01， Ta=3。72×10^5， Re=4。4×10^3;表面張力Ma數(shù)取15~40。

3.1 非均勻旋轉(zhuǎn)磁場對液橋熔體對流的影響

二極對非均勻旋轉(zhuǎn)磁場作用下，液橋熔體的最大周向?qū)α魉俣鹊玫教岣撸畲筝S向?qū)α魉俣鹊玫捷^好的抑制。圖3描述了Ma數(shù)由15逐漸增加到40的過程中，二極對非均勻旋轉(zhuǎn)磁場(7 mT、50 Hz)對液橋熔體對流速度的影響。與無磁場條件相比，二極對非均勻旋轉(zhuǎn)磁場作用下，Ma=30時液橋熔體的最大周向速度增加了4。75倍，最大軸向速度降低了28。5%;Ma=35時液橋熔體的最大周向速度增加了3。48倍，最大軸向速度降低了25%;Ma=40時液橋熔體的最大周向速度增加了2。75倍，最大軸向速度降低了22%。

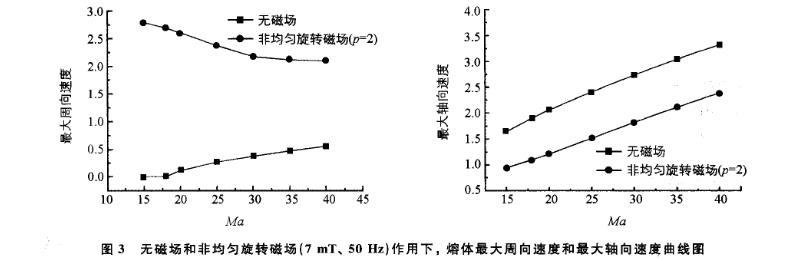
圖3 無磁場和非均勻旋轉(zhuǎn)磁場(7 mT、50 Hz)作用下，熔體最大周向速度和最大軸向速度曲線圖

本文所采用的旋轉(zhuǎn)磁場有限長-α模型考慮到洛侖茲力的所有分量，其中周向洛倫茲力對熔體對流的影響最大，即外加旋轉(zhuǎn)磁場會對熔體產(chǎn)生周向攪拌作用。數(shù)值結(jié)果表明，微重力下二極對非均勻旋轉(zhuǎn)磁場使液橋熔體周向流動得到加強(qiáng)，該結(jié)論與理論分析是一致的。此外，熔體軸向?qū)α魉俣鹊玫接行б种疲芯勘砻鳎O對非均勻旋轉(zhuǎn)磁場對液橋熔體兩方面的作用效果均有助于控制液橋熔體流，將其轉(zhuǎn)變?yōu)槎S軸對稱定常流動。

3.2 非均勻旋轉(zhuǎn)磁場作用下液橋的對流特性分析

微重力環(huán)境下，無磁場時熔體表面張力對流隨著Ma數(shù)的增大將會產(chǎn)生失穩(wěn)，首先由二維軸對稱定常流轉(zhuǎn)變?yōu)槿S定常流。Ma=40時，熔體對流已經(jīng)經(jīng)歷過第一次失穩(wěn)。此時液橋熔體對流為定常三維流動。圖4描述了無磁場條件下，液橋熔體Z=0。5H切面上的溫度等值線和流線圖。從圖4(a)中可以看出，熔體Z=0。5H切面上溫度分布具有明顯的非軸對稱性，且在自由表面附近分別形成了一對熱區(qū)和一對冷區(qū)。同時，從4(b)中看到，Z=0。5H切面上的流線亦為明顯的渦流結(jié)構(gòu):在自由表面附近，熔體從低溫區(qū)流向高溫區(qū)，這一流動與自由表面上軸向表面張力驅(qū)動流體從高溫區(qū)流向低溫區(qū)是相反的，結(jié)果表明半浮區(qū)液橋的周向流動并不是表面張力驅(qū)動的。表面張力只是作為周向流動的微弱的反作用力而存在。

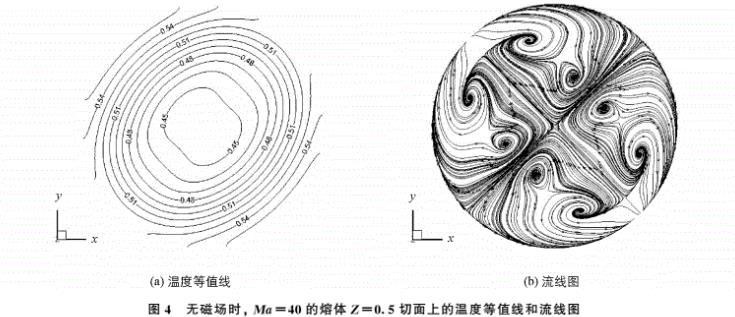
(a) 溫度等值線 (b) 流線圖

圖4 無磁場時， Ma=40的熔體Z=0。5H切面上的溫度等值線和流線圖

在外加二極對非均勻旋轉(zhuǎn)磁場(7 mT、50 Hz)作用下，浮區(qū)液橋失穩(wěn)后的三維非軸對稱的對流特性得到有效地改善。圖5為二極對非均勻旋轉(zhuǎn)磁場作用下，Ma=40時的半浮區(qū)液橋在Z=0。5H切面上的溫度等值線和流線圖。從5(a)中可以看出，二極對非均勻旋轉(zhuǎn)磁場的周向攪拌作用下，熔體Z=0。5H切面上的溫度以中心軸為中心呈現(xiàn)出明顯的軸對稱分布特性;熔體在Z=0。5H切面上由液橋中心向自由表面流動，形成周向渦流結(jié)構(gòu)，如圖5(b)所示。研究結(jié)果表明，二極對非均勻旋轉(zhuǎn)磁場的周向攪拌作用下，Ma=40時熔體的三維非軸對稱表面張力對流得到有效地控制，此時二維軸對稱流動特性明顯。

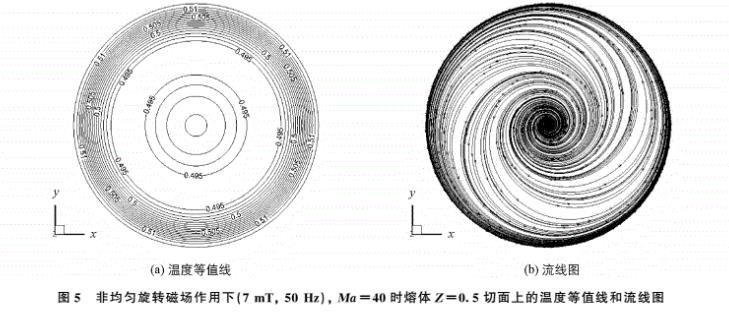
(a) 溫度等值線 (b) 流線圖

圖5 非均勻旋轉(zhuǎn)磁場作用下(7 mT， 50Hz)， Ma=40時熔體Z=0。5H切面上的溫度等值線和流線圖

4 結(jié)論

本文采用有限體積法數(shù)值研究了微重力環(huán)境下，外加二極對非均勻旋轉(zhuǎn)磁場(7 mT、50 Hz)對半浮區(qū)液橋表面張力對流特性的影響。研究結(jié)果表明，無磁場作用下，半浮區(qū)液橋隨著Ma數(shù)(15—40)的逐漸增加將會產(chǎn)生首次失穩(wěn)由二維軸對稱流動轉(zhuǎn)變?yōu)槿S定常流動。外加二極對非均勻旋轉(zhuǎn)磁場的周向攪拌作用下，液橋熔體的最大周向速度得到加強(qiáng)，同時熔體最大軸向?qū)α魉俣鹊玫接行б种疲撟饔眯Ч欣诳刂埔簶蛉垠w的三維表面張力對流并將其轉(zhuǎn)變?yōu)槎S軸對稱流動。因此，外加二極對非均勻旋轉(zhuǎn)磁場可以作為一種控制液橋熔體表面張力對流的有效手段。